C14.2 - Descompuneri în factori utilizând reguli de calcul în ℝ (formule de calcul prescurtat)

---

Definiție

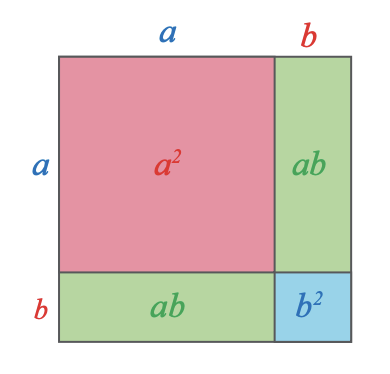
1. Privește cu atenție imaginea și stabilește care dintre afirmații este corectă.

• „Aria pătratului mare este $a^2 + 2ab + b^2$.”
• „Aria pătratului mare este $(a + b)^2$.”

2. Este adevărată relația: $a^2 + 2ab + b^2 = (a + b)^2$?

3. Completează expresiile astfel încât să obții relații adevărate:

• a) $a^2 - 2ab + b^2 = (\dots)^2$;
• b) $a^2 - b^2 = (a - \dots)(\dots + b)$.

Important

• O metodă de descompunere în factori este utilizarea formulelor de calcul prescurtat.

Formulele de calcul prescurtat pot fi scrise și astfel:

• $a^2 + 2ab + b^2 = (a + b)^2$ (pătratul sumei)
• $a^2 - 2ab + b^2 = (a - b)^2$ (pătratul diferenței)
• $a^2 - b^2 = (a - b)(a + b)$ (diferența de pătrate)

Exemplul 1

Descompune în factori expresiile algebrice: $E(x) = x^2 + 6x + 9$ și $E(x, y) = 4x^2 - 12xy + 9y^2$, $E(x, y) = 4x^2 - y^2$.

Soluție: $E(x) = x^2 + 6x + 9$ este o expresie algebraică care are trei termeni. Mă pot gândi la una dintre formulele $a^2 + 2ab + b^2 = (a + b)^2$ sau $a^2 - 2ab + b^2 = (a - b)^2$. Pentru aceasta trebuie să identific $a^2$, $b^2$ și $2ab$.

Analiza procesului:

Pentru că $2ab$ are semnul plus:

$E(x) = x^2 + 6x + 9 = (x + 3)^2$

• Identificarea termenilor:
  • $a^2 = x^2 \Rightarrow a = x$
  • $b^2 = 9 \Rightarrow b = 3$
• Verificarea termenului dublu:
  • $2ab = 2 \cdot x \cdot 3 = 6x$

Concluzie: Se poate folosi formula $a^2 + 2ab + b^2 = (a + b)^2$

---

Exemplul 2

$E(x, y) = 4x^2 - 12xy + 9y^2$ este o expresie algebraică care are trei termeni. Mă pot gândi la formulele $a^2 + 2ab + b^2 = (a + b)^2$ și $a^2 - 2ab + b^2 = (a - b)^2$. Pentru aceasta trebuie să identific $a^2, b^2$ și $2ab$.

Analiza procesului:

Pentru că $2ab$ are semnul minus:

$E(x,y) = 4x^2 - 12xy + 9y^2 = (2x - 3y)^2$

• Identificarea termenilor:
  • $a^2 = 4x^2 \Rightarrow a = 2x$
  • $b^2 = 9y^2 \Rightarrow b = 3y$
• Verificarea termenului dublu:
  • Verific dacă $2ab = 12xy$
  • $2ab = 2 \cdot 2x \cdot 3y = 12xy$

Concluzie: Se poate folosi formula $a^2 - 2ab + b^2 = (a - b)^2$

---

Exemplul 3

$E(x, y) = 4x^2 - y^2$ este o expresie algebraică care are doi termeni și între ei semnul minus. Mă gândesc la formula $a^2 - b^2 = (a - b)(a + b)$. Pentru aceasta trebuie să identific $a^2$ și $b^2$

Analiza procesului:

$E(x,y) = 4x^2 - y^2 = (2x + y)(2x - y)$

• Identificarea termenilor:
  • $a^2 = 4x^2 \Rightarrow a = 2x$
  • $b^2 = y^2 \Rightarrow b = y$

Concluzie: Se poate folosi formula $a^2 - b^2 = (a + b)(a - b)$

---