Skip to main content

Portofoliu (partea I)

Organizarea portofoliului​

Ce vei face?​

Un portofoliu care te ajută la organizarea noțiunilor esențiale pentru a te ajuta să apreciezi cât ai progresat.

Când vei face?​

Termenul limită este 8 martie 2026. Portofoliul trebuie să fie completat până atunci, urmând ca verificarea și notarea acestora să fie realizată în săptămâna următoare (9 - 13 martie 2026).

Cum vei face?​

Vei rezolva diferite exerciții și probleme propuse din fiecare capitol.

Poți completa portofoliul și cu exerciții și probleme propuse din alte surse, rezolvate de tine extra.

E1 - Mulțimi definite printr-o proprietate a elementelor lor​

cerințǎ

Determină elementele următoarelor mulțimi:

a)  A={x∈Z  ∣  x divide pe 20}a)\;A = \{x \in \mathbb{Z} \; | \; \text{x divide pe 20}\}

b)  B={x∈N  ∣  10x∈N}b)\;B = \{x \in \mathbb{N} \; | \; \dfrac{10}{x} \in \mathbb{N}\}

c)  C={x∈Z  ∣  152x+1∈Z} c)\;C = \{x \in \mathbb{Z} \; | \; \dfrac{15}{2x+1} \in \mathbb{Z}\}

d)  D={x∈Z  ∣  x+1x∈N}d)\;D = \{x \in \mathbb{Z} \; | \; \dfrac{x+1}{x} \in \mathbb{N}\}

E2 - Intervale numerice și reprezentarea lor pe axa numerelor​

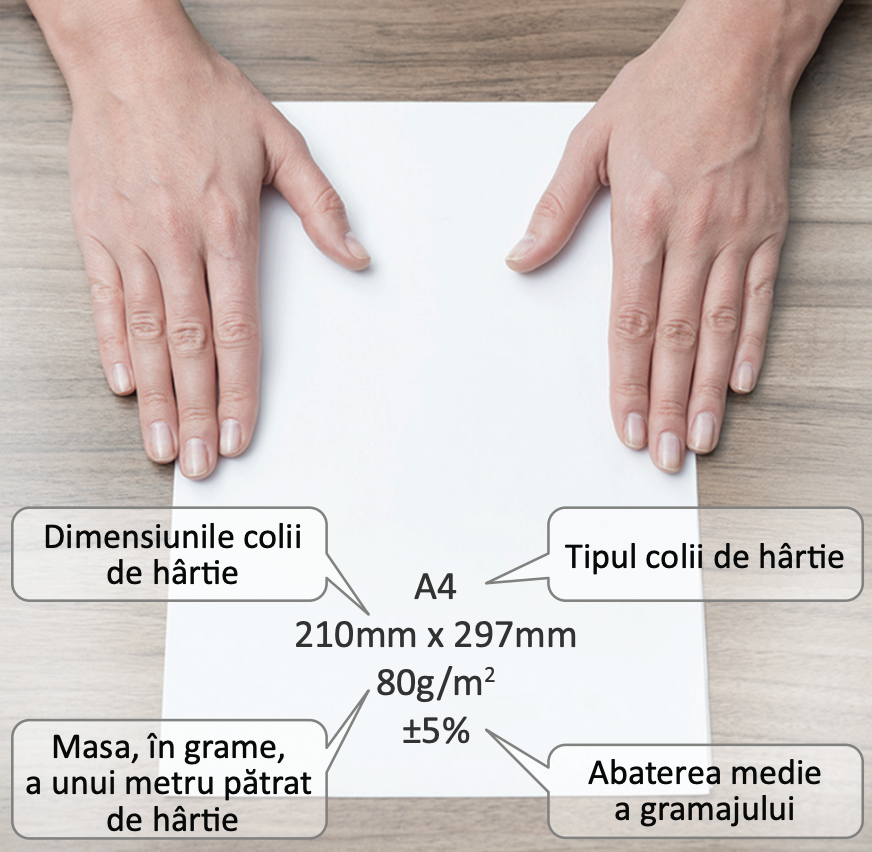
Smith family bathroom schedule

cerințǎ

În imaginea alăturată este prezentată schița pentru ultima copertă a unui caiet și semnificația înscrisurilor de pe această copertă. Știind că acest caiet conține 100 de foi stabilește dacă masa acestui caiet, exprimată în grame, aparține intervalului (100, 500).

E3 - Intersecția și reuniunea intervalelor​

cerințǎ

Maria vrea să meargă la cabinetul medical și la cabinetul stomatologic pentru un control de rutină. În imaginea de mai jos sunt afișate programele celor două cabinete. Consultându-și programul din săptămâna următoare, constată că cea mai bună zi pentru mersul la control este miercuri.

a) În ce interval orar sunt deschise ambele cabinete, miercuri?

b) Dacă fiecare control durează două ore, iar drumul între cele două cabinete durează o oră, care este ultima oră la care Maria poate intra la unul dintre cabinete astfel încât să fie sigură că poate efectua și celălalt consult în aceeași zi?

Smith family bathroom schedule

cerințǎ

Pentru fiecare număr natural nenul nn, definim intervalul In=[12n,1n]I_n = \left[\dfrac{1}{2n}, \dfrac{1}{n}\right].

a) Calculează I1∩I2;  I2∩I3;  I3∩I4I_1\cap I_2; \; I_2\cap I_3; \; I_3\cap I_4.

b) Calculează I1∪I2∪I4I_1 \cup I_2 \cup I_4.

E4 - Inecuații de forma ax+b≥0(≤,<,>)ax + b \geq 0 (\leq , \lt , \gt), unde a,b∈Ra, b \in \mathbb{R}​

cerințǎ

Determină mulțimile:

a)  A={x∈R  ∣  5x−8≥2x+3}a)\;A = \{x \in \mathbb{R} \; | \; 5x-8\geq 2x+3\}

b)  B={x∈R  ∣  2x+35<1}b)\;B = \{x \in \mathbb{R} \; | \; \dfrac{2x+3}{5} < 1\}

c)  C={x∈R  ∣  ∣x+1∣<5}c)\;C = \{x \in \mathbb{R} \; | \; |x+1| < \sqrt{5}\}

E5 - Operații cu numere reale exprimate prin litere (adunare și scădere)​

cerințǎ

Redu termenii asemenea în următoarele cazuri:

a)  3x−5y+3y−xa)\; 3x − 5y + 3y − x

b)  4x2+3x+2−3x2−2x+3b)\; 4x^2 + 3x + 2 − 3x^2 − 2x + 3

c)  7a+3b−5b−8ac)\; 7a + 3b − 5b − 8a

d)  10x2+5x−1−7x2−3x+8d)\; 10x^2 + 5x − 1 − 7x^2 − 3x + 8

e)  −6ax−0,2a2+2x+1,2a2+3ax−2xe)\; −6ax − 0,2a^2 + 2x + 1,2a^2 + 3ax − 2x

f)  2x2+y2−4xy−4y2+xy−x2+y2f)\; 2x^2 + y^2 − 4xy − 4y^2 + xy − x^2 + y^2

g)  −x3y+x2y2+x3y+2xy−x2y2+1−2xyg)\; −x^3y + x^2y^2 + x^3y + 2xy − x^2y^2 + 1 − 2xy

h)  2x3−y3+3x2+y3h)\; 2x^3 − y^3 + 3x^2 + y^3

E6 - Operații cu numere reale exprimate prin litere (înmulțirea, împărțirea, ridicarea la putere)​

cerințǎ

Calculează, reducând termenii asemenea:

a)  (x+1)(x2−x+1)a)\; (x + 1)(x^2 − x + 1)

b)  (x−2)(x2+2x+4)b)\; (x − 2)(x^2 + 2x + 4)

c)  (x−y)(x2+xy+y2)c)\; (x − y)(x^2 + xy + y^2)

d)  (x+1)(x3−x2+x−1)d)\; (x + 1)(x^3 − x^2 + x − 1)

e)  (x−1)(x3+x2+x+1)e)\; (x − 1)(x^3 + x^2 + x + 1)

f)  (x+1)(x4−x3+x2−x+1)f)\; (x + 1)(x^4 − x^3 + x^2 − x + 1)

E7 - Formule de calcul prescurtat​

cerințǎ

Calculează:

a)  (2+3)2a)\; (2 + \sqrt{3})^2

b)  (23−1)2b)\; (2\sqrt{3} - 1)^2

c)  (3+1)(3−1)c)\; (\sqrt{3} + 1)(\sqrt{3} - 1)

d)  (3−2)(3+2)d)\; (\sqrt{3} - \sqrt{2})(\sqrt{3} + \sqrt{2})

e)  (5+2)(5−2)e)\; (\sqrt{5} + 2)(\sqrt{5} - 2)

f)  (32−23)2f)\; (3\sqrt{2} - 2\sqrt{3})^2

g)  (33+22)2g)\; (3\sqrt{3} + 2\sqrt{2})^2

h)  (32−23)(32+23)h)\; (3\sqrt{2} - 2\sqrt{3})(3\sqrt{2} + 2\sqrt{3})

E8 - Aria unui dreptunghi​

cerințǎ

Un dreptunghi are perimetrul de 14 cm. Dacă diagonala dreptunghiului este de 5 cm, determină aria acestui dreptunghi.

E9 - Ecuații de forma ax2+bx+c=0ax^2 + bx + c = 0, unde a∈R∗,b,c∈Ra \in \mathbb{R}^{*}, b, c \in \mathbb{R}​

cerințǎ

Rezolvă în mulțimea numerelor reale următoarele ecuații:

a)  x2+4x+3=0;a)\; x^2 + 4x + 3 = 0;

b)  x2+7x+12=0;b)\; x^2 + 7x + 12 = 0;

c)  x2−11x+24=0;c)\; x^2 - 11x + 24 = 0;

d)  4x2+4x+3=0d)\; 4x^2 + 4x + 3 = 0

e)  3x2−2x+5=0e)\; 3x^2 - 2x + 5 = 0

f)  6x2−7x+2=0f)\; 6x^2 - 7x + 2 = 0

g)  10x2+29x+10=0g)\; 10x^2 + 29x + 10 = 0

h)  x2+2x+2=0h)\; x^2 + 2x + 2 = 0

i)  9x2−6x−3=0i)\; 9x^2 - 6x - 3 = 0

E10 - Expresii algebrice​

cerințǎ

Se consideră expresia algebrică E(x)=x2−4x+10E(x) = x^2 − 4x + 10, unde xx este număr real. Determină cea mai mică valoare pe care o poate avea E(x)E(x)

E11 - Perimetrul unui triunghi​

cerințǎ

Suma lungimilor catetelor unui triunghi dreptunghic este egală cu 14 cm, iar aria triunghiului este egală cu 24 cm². Determină perimetrul triunghiului.

E12 - Fracții algebrice​

cerințǎ

Se consideră fracția algebrică E(x)=x2−10x+25x3−25xE(x) = \dfrac{x^2 - 10x + 25}{x^3 - 25x}, unde xx este număr real.

a) Arată că x3−25x=x(x−5)(x+5)x^3 - 25x = x(x - 5)(x + 5)

b) Determină mulțimea de definiție a fracției algebrice E(x)E(x)

c) Arată că E(x)=x−5x(x+5)E(x) = \dfrac{x - 5}{x(x + 5)}

d) Rezolvă în mulțimea numerelor reale ecuația E(x)=1x(x+5)E(x) = \dfrac{1}{x(x + 5)}

E13 - Operații cu fracții algebrice (adunarea și scăderea)​

cerințǎ

Pentru xx aparținând mulțimii de definiție a fiecărei fracții algebrice, efectuează:

a)  3x2+x−xx−2+10x2−4a) \; \dfrac{3x}{2+x} - \dfrac{x}{x-2} + \dfrac{10}{x^2-4}

b)  xx+3−(x+2x2−9−1x−3)b) \; \dfrac{x}{x + 3} - \left(\dfrac{x + 2}{x^2 - 9} - \dfrac{1}{x - 3}\right)

c)  1x+1−(x−2x2−x−x+2x)c) \; \dfrac{1}{x + 1} - \left(\dfrac{x - 2}{x^2 - x} - \dfrac{x+2}{x}\right)

d)  4+x22x−x2x2+2x−x22x+4d) \; \dfrac{4 + x^2}{2x} - \dfrac{x^2}{x^2+2x} - \dfrac{x^2}{2x+4}

E14 - Operații cu fracții algebrice (înmulțirea și împărțirea)​

cerințǎ

Se consideră expresia algebrică E(x)=(1x+1+11−x):1x2−1E(x) = \left(\dfrac{1}{x + 1} + \dfrac{1}{1 - x}\right) : \dfrac{1}{x^2 - 1}, unde x∈R∖{−1,1}x \in \mathbb{R} \setminus \{−1, 1\}.

Arată că E(x)E (x) este un număr întreg, pentru orice număr x∈R∖{−1,1}x \in \mathbb{R} \setminus \{−1, 1\}.

cerințǎ

Se consideră expresia algebrică:

E(x)=((1x+2)2−(1x+3)2)⋅(x2+5x+64x+10)2−18x−20, unde x∈R∖{−3,−52,−2,52}E(x) = \left( \left( \dfrac{1}{x+2} \right)^2 - \left( \dfrac{1}{x+3} \right)^2 \right) \cdot \left( \dfrac{x^2+5x+6}{4x+10} \right)^2 - \dfrac{1}{8x-20}, \text{ unde } x \in \mathbb{R} \setminus \left\{ -3, -\frac{5}{2}, -2, \frac{5}{2} \right\}

a) Arată că E(x)=550−8x2E(x) = \dfrac{5}{50-8x^2} pentru orice x∈R∖{−3,−52,−2,52}x \in \mathbb{R} \setminus \left\{ -3, -\frac{5}{2}, -2, \frac{5}{2} \right\}

b) Rezolvă în mulțimea R∖{−3,−52,−2,52}\mathbb{R} \setminus \left\{ -3, -\frac{5}{2}, -2, \frac{5}{2} \right\} ecuația E(x)=15+2xE(x) = \frac{1}{5+2x}

c) Rezolvă în mulțimea R∖{−3,−52,−2,52}\mathbb{R} \setminus \left\{ -3, -\frac{5}{2}, -2, \frac{5}{2} \right\} inecuația E(x)≥0E(x) \geq 0

cerințǎ

Se consideră expresia algebrică E(x)=(2x2+1+x2+3x3−x2+x−1):x2−1x2+1E(x) = \left( \dfrac{2}{x^2+1} + \dfrac{x^2+3}{x^3-x^2+x-1} \right) : \dfrac{x^2-1}{x^2+1}, unde x∈R∖{−1,1}x \in \mathbb{R} \setminus \{-1, 1\}

a) Arată că E(x)=x+1(x−1)2E(x) = \dfrac{x+1}{(x-1)^2}, pentru orice număr x∈R∖{−1,1}x \in \mathbb{R} \setminus \{-1, 1\}

b) Rezolvă în mulțimea numerelor reale inecuația 1E(x)≤0\frac{1}{E(x)} \leq 0

E15 - Prisma dreaptă​

cerințǎ

În imaginea de lângă este schița unui bloc având forma unui paralelipiped dreptunghic. Trebuie construită o scară exterioară care să pornească din punctul A și să ajungă în punctul A', urmând traseul din schiță. Se știe că dimensiunile blocului sunt AA' = 30 m, AB = 12 m și BC = 24 m.

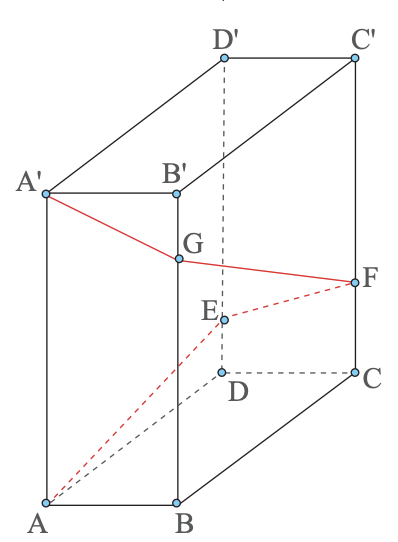
Figura 13

a) Determină lungimea minimă a scării.

b) Determină lungimile segmentelor DE, CF și BG pentru care lungimea scării este minimă

E16 - Piramida​

cerințǎ

Se consideră patru piramide, una cu baza triunghi, una cu baza patrulater, una cu baza pentagon și una cu baza hexagon.

a) Realizează câte un desen pentru fiecare tip de piramidă.

b) Determină numărul de vârfuri (vârful piramidei și vârfurile bazei) vv, pentru fiecare piramidă.

c) Determină numărul total de fețe (baza și fețele laterale) ff, pentru fiecare piramidă.

d) Determină numărul de muchii (muchiile bazei și muchiile laterale) mm, pentru fiecare piramidă.

e) Verifică, pentru fiecare piramidă în parte, relația v−m+f=2v−m+f = 2 (formula lui Euler pentru poliedre).

Date Biografice

Leonhard Euler, matematician și fizician elvețian, s-a născut în Basel, Elveția (1707) și a decedat în Sankt Petersburg, Rusia (1783).

E17 - Cilindrul circular drept​

cerințǎ

În figura de mai jos este reprezentată desfășurarea unui cilindru circular drept.

a) Dacă lungimea cercului de la baza cilindrului este 14π  cm14 \pi \; cm, ce lungime are segmentul AA1AA_1?

b) Știind că aria dreptunghiului AA1D1DAA_1D_1D este egală cu 70π  cm270\pi \; cm^2, determină lungimea generatoarei cilindrului

Figura 14

prof. ing. BRIȘAN Andrei-Sebastian